WIND ENERGY
AND POWER
Here we present the physical principles of power calculation.
This requires knowledge of physics and mathematics. These explanations are only for those who want to know the scientific-physical context.
These explanations are only for those who want to know the scientific-physical context. The yield is good when the flow is laminar. If the flow is disturbed by obstacles, the wind becomes turbulent and is then not so well suited for optimal use by rotor profiles.
Wind:
Wind is moving air in nature. Internationally, wind is measured at 10 m above ground and given in 10-minute averages in m/s.
The 10-minute averages do NOT take gusts into account!
For a given location of the KUKATE, the following factors are effective:
- Wind speed at 10m mast height
- Wind direction,
- Degree of turbulence (disturbing buildings, trees)
- Air temperature (viscosity)
- Density of the air (height of the site above sea level)
- Wind frequency and wind speed distribution at the site
Wind measurement and locations:
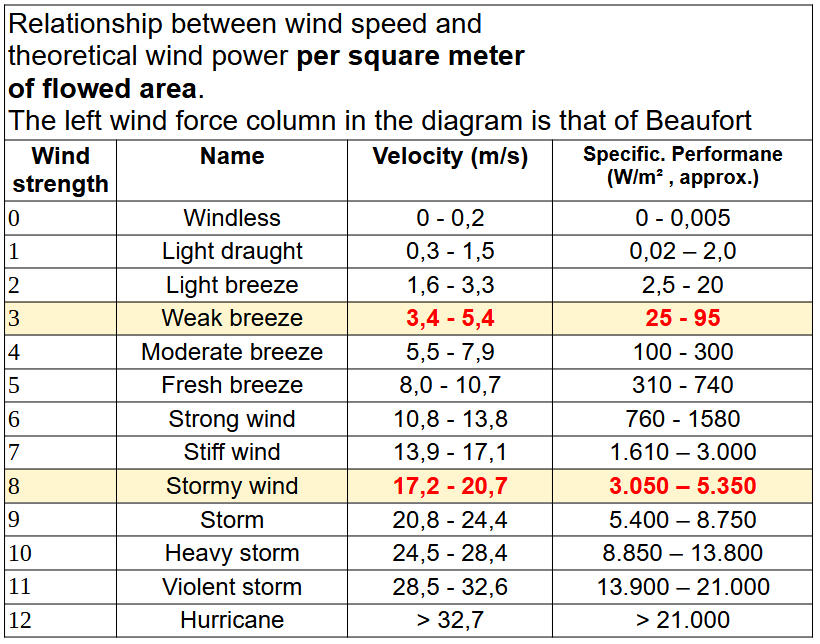
Measurements are often taken according to the old Beaufort scale in “wind forces” (Bf) from 1-12.
Our KUKATE34 rotors start turning at 3 m/s to 4 m/s (2-3 Bf). At 7 m/s (4Bf) they have reached their maximum performance.
If the wind blows stronger, they are slowly swung out of the wind so that the pump is not overloaded.
Wherever wind often blows at more than 4m/s, we can use it for our pumps. Coastal regions of the mainland, islands and flat, exposed terrain are ideal for the operation of water pumps.
Wind energy and wind power:
A moving air mass has kinetic energy.
Dividing the wind energy E = 1/2- x m x v²
(E is the energy in Ws or Nm/s², m is the air mass in kg and v is the wind speed).
by a time interval (here by one second), the wind power in watts is obtained.
The following formula makes the relationships clear:
PWind = 1/2 x ρ x A x v³
(P is the power in watts, ρ is the air density in kg/m³, A is the vertical flow area in m² and v is the wind speed in m/s).
This formula is used to calculate the power of an air flow under normal conditions.
The wind speed is in this formula with the 3rd power. That is why an unimaginably steep increase in power with wind speed occurs.
The table shows the increase of power with increasing wind speed: e.g. at 20 m/s wind speed extreme 5000 Watt/m² – but at 4 m/s wind speed not even 40 W/m²!
Technical usability and efficiency:
These theoretical values of wind power per square meter in the 4th column must be multiplied by the efficiency of the rotor (approx. 0.3 for a Westernmill rotor), the efficiency of the pump (approx.0.8) and that of the connecting rod and linkage (approx. 0.8). This product then gives an overall efficiency of approximately 0.2.
This means: If the shaft of the rotor of the KUKATE34 produces 500 watts at a wind speed of 6-7 m/s, 500 W x 0.2 = 100 watts effective power for the pump.
Formula: Power is work divided by time
The power of the 100 W pump in liters per second is then the lifting work for the water (water mass (1 kg) x acceleration due to gravity (9.8 m/s²) x pump height (10 m) divided by the time interval of one second (1 s).
Calculated, this gives (1 kg x 9.8 m/s² x 10m)/s = 980 Nm/s = 98 watts, which is about 100 W.
Illustration of performance on human performance:
An average hard-working man can permanently perform about 70 watts during his work. If he works 10 hours without interruption per day, that is 700 Wh per person.
The KUKATE rotor generates 500 watts of power on the wave at 7 m/s wind – 24 hours a day. That’s 12,000 Wh per day.
So the rotor performs as much as 19 continuously hard working people (12000 Wh / 700 Wh), even on Sundays!
Shaft power, pump power and control of the KUKATE34 rotor:
The 500 W shaft power of the 3.4 m diameter rotor with an effective effective effective area of 6.6 m² of the KUKATE34 is achieved at 7 m/s. The pump then delivers one liter of water per second at an efficiency of 0.2. This is explained under the bullet point “Technical usability and efficiency”.
This is 3600 liters of water per hour from a depth of 10 meters and 86400 liters per day.
At 9 m/s, the rotor already has a power of 1500 W. This is too much load for the pump.
Therefore, from a wind speed of 7 m/s, the control and side vane combination swing the rotor out of the wind. In this way, the pump is not overloaded. In the storm, the flags are folded on an angle of 30 degrees. The rotor is then blown at an angle from the side and offers little resistance to the storm. Its performance is then very limited.
